LH26 - La LH en pixel art
Aujourd'hui, je voudrais parler de plans projectifs finis. Ça a peut-être pas l'air très intéressant, mais moi je trouve ça absolument magnifique, et en plus ça permet de comprendre comment fonctionne le jeu de société Dobble.
En géométrie, on manipule des points et des droites. Au collège et au lycée, on a fait de la géométrie dans le plan (ou l'espace euclidien). Mais il est possible de définir d'autres espaces plus exotiques qui vérifient à peu près les mêmes propriétés. Notamment, on voudrait la propriété $(P_1)$ : entre deux points distincts passe toujours exactement une droite.
Ici, on va essayer de construire un tel espace fini (avec un nombre fini de points et de droites).
On peut commencer très simplement avec cet espace, constitué de $2$ points et $1$ droite :
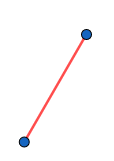
Cet espace vérifie évidemment la propriété $(P_1)$. Mais c'est pas très intéressant. On voudrait qu'il y ait plus de points. Plus précisément, on voudrait la propriété $(P_2)$ : il existe des points non alignés (i.e. $3$ points qui ne sont pas traversés par une même droite). Sans cette propriété, on obtient juste une droite avec un certain nombre de points dessus. Donc on ajoute un nouveau point non aligné avec les deux premiers :
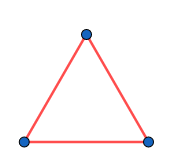
C'est toujours pas très satisfaisant. En fait, on pourrait construire un espace du même genre pour n'importe quel nombre de points, en reliant chaque paire de points par une droite (donc chaque droite passerait par seulement deux points). Pour éviter ça, on impose la propriété $(P_3)$ : chaque droite passe par au moins $3$ points. Là, ça se complique. Vous pouvez essayer, et vous allez voir que c'est pas évident de satisfaire toutes les contraintes. Voici comment faire. On commence par ajouter un point à l'une des droites :
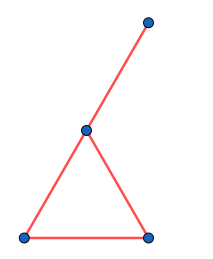
Pour que la propriété $(P_1)$ soit vérifiée, il faut ajouter une droite. Puis un point pour vérfier la propriété $(P_3)$. Pourquoi je mets le point ici ? Pour que ça marche.
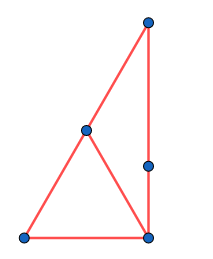
C'est toujours pas fini, il y a deux points qui ne sont pas reliés. En continuant, à condition de bien s'y prendre, on obtient ça :
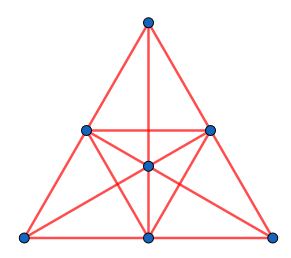
Là, on pourrait penser qu'il y a trois droites qui passent par $2$ points seulement (les droites qui relient les milieux des côtés du grand triangle). Mais en fait, on peut considérer ces trois droites comme une seule droite, qui passe alors bien par $3$ points. Pour que ça soit plus visible, on peut la remplacer par un cercle :
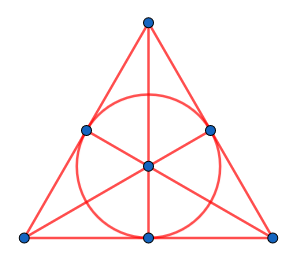
Et là, on vérifie bien toutes les propriétés.
L'espace qu'on a obtenu s'appelle le plan de Fano. Si on récapitule, il vérifie les merveilleuses propriétés suivantes (on peut les voir facilement sur le dessin) :
Notez que dans le plan euclidien $\mathbb R^2$, le troisième point est presque toujours vrai, mais il y a l'exception des droites parallèles. Dans le plan de Fano, pas d'exception, tout se passe très bien.
Dans le plan de Fano, aucun point ni aucune droite ne joue un rôle particulier. Tout est parfaitement symétrique. Aussi, les notions de point et de droite sont parfaitement interchangeables : j'aurais pu décider d'appeler les points bleus des droites, et les droites rouges des points, et on aurait eu exactement les mêmes propriétés. Par exemple, la propriété "entre deux points distincts passe toujours exactement une droite" devient "entre deux droites distinctes passe toujours exactement un point", ou autrement dit "deux droites distinctes ont toujours exactement un point d'intersection". On parle de dualité projective.
Plus généralement, pour tout entier $q \geqslant 2$ qui est une puissance d'un nombre premier, on peut construire un plan projectif à $1+q+q^2$ points et $1+q+q^2$ droites qui vérifie le même genre de propriétés absolument magnifiques (notamment, chaque droite contient $q+1$ points et chaque point est traversé par $q+1$ droites). Bon par contre, on ne peut en général pas les représenter élégamment dans le plan euclidien, comme on l'a fait pour le plan de Fano. Celui-ci est le plus petit plan projectif : il est obtenu avec $q=2$.
~~Je ne comprends pas pourquoi des milliards d'êtres humains vénèrent diverses divinités, alors qu'à la place ils pourraient vénérer les plans projectifs finis, qui sont au moins aussi parfaits, et qui en plus ont le bon goût de vraiment exister.~~
Mais, me demanderiez-vous, peut-on construire un plan projectif fini dont le nombre de points n'est pas de la forme $1+q+q^2$ où $q$ est une puissance d'un nombre premier ? Eh bien, c'est un problème ouvert. Plus précisément, on sait que le nombre de points est forcément de la forme $1+q+q^2$, mais on ne sait pas si $q$ est forcément une puissance d'un nombre premier. Par exemple, on ne sait pas s'il existe un plan projectif fini à $157=1+12+12^2$ points.
Dans les plans projectifs, on a toujours la dualité projective qu'on avait vue pour le plan de Fano et qui permet d'interchanger les points et les droites. Notamment, ça veut dire que si on démontre un théorème portant sur les plans projectifs, on peut échanger les mots "point" et "droite", et on obtient automatiquement un nouveau théorème.
Encore plus généralement, on peut définir un espace projectif à partir de n'importe quel espace vectoriel. Le plan de Fano est obtenu à partir de l'espace vectoriel $\mathbb F_2^3$. Le $2$ est lié au fait que $q=2$, et le $3$ est lié au fait que c'est un plan. On parle de plan projectif lorsque l'espace vectoriel est de dimension $3$, et d'espace projectif en général. Ceux-ci ont des propriétés un peu moins élégantes que les plans projectifs.
Sans rentrer dans les détails, on les construit en enlevant l'origine de l'espace vectoriel, et en identifiant les points colinéaires.
Et pourquoi ça s'appelle des espaces projectifs ? Parce qu'on peut aussi les construire à partir d'espaces affines, en ajoutant des points pour forcer les droites parallèles à s'intersecter. Si on part de l'espace affine usuel $\mathbb R^3$, les points qu'on ajoute sont "à l'infini". Et c'est ce qu'il se passe quand on projette un espace 3D sur un dessin en 2D : les lignes parallèles (par exemple, les bordures de la route sur le dessin ci-dessous) s'intersectent en un point de fuite situé à l'infini. On peut donc voir le dessin 2D comme une représentation de l'espace projectif associé à l'espace affine $\mathbb R^3$.
Les espaces projectifs finis servent en cryptographie (c'est pour ça qu'il y a un cours d'ACCQ dans lequel on voit ça), mais je vais plutôt présenter une application beaucoup plus simple et concrète : le Dobble.
Le Dobble est un jeu de société constitué de $55$ cartes contenant chacune $8$ petits dessins. Ces cartes ont la propriété remarquable suivante : si on prend deux cartes quelconques, elles ont toujours exactement un dessin en commun. Par exemple, sur les deux cartes ci-dessus, l'unique dessin commun aux deux cartes est le point d'interrogation. Le but du jeu est, en gros, de trouver le dessin commun à deux cartes le plus rapidement possible.
Je sais pas vous, mais moi, quand j'ai entendu les règles pour la première fois, ça me semblait très contre-intuitif qu'une telle chose soit possible. Mais la géométrie projective permet une telle prouesse.
En effet, si on décide d'appeler les dessins des "points" et les cartes des "droites", la propriété remarquable devient : deux droites distinctes ont toujours exactement un point d'intersection. Ça vous rappelle quelque chose ?
Eh oui, les cartes et les dessins du Dobble forment un plan projectif fini ! Bon, si vous êtes perspicace, vous avez peut-être remarqué que $55$ n'est pas de la forme $1+q+q^2$. En fait, il devrait y avoir $57=1+7+7^2$ cartes, mais deux cartes ont été enlevées pour optimiser le processus de fabrication (oui, c'est moche la vraie vie). Ça ne change rien au fait qu'il y a toujours exactement un symbole commun entre deux cartes, mais ça rend le jeu un peu moins symétrique (certains dessins sont légèrement sous-représentés).
Par contre, il y a bien $57$ dessins distincts. Et aussi, on sait que le Dobble doit vérifier la propriété suivante (qui ne sert à rien dans les règles du jeu) : si on prend deux dessins distincts, il y a exactement une carte qui contient ces deux dessins (modulo les deux cartes manquantes).
Bon, je sais pas si c'était très clair, donc pour rendre ça plus concret on va fabriquer un mini-Dobble basé sur le plan de Fano. Il contiendra donc seulement $7$ cartes et $7$ dessins, et il y aura $3$ dessins par carte. En fait, c'est très simple à faire : il suffit d'associer un dessin à chaque point du plan de Fano :
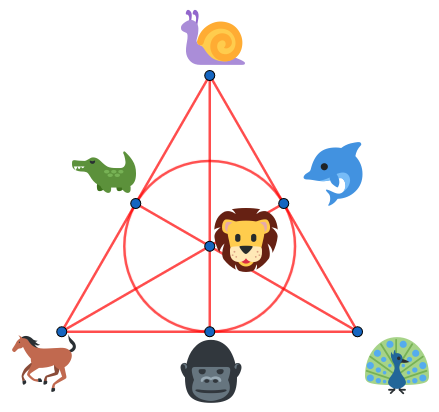
et ensuite on créé une carte pour chaque droite du plan de Fano, qui contient les dessins par lesquels passe la droite (désolé mes cartes sont très moches) :
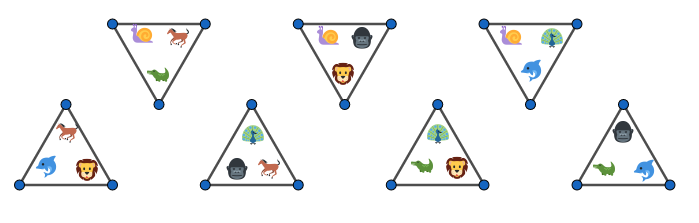
Et voilà, vous pouvez vous convaincre qu'il y a bien toujours exactement un dessin en commun entre deux cartes !
Pour conclure, j'aimerais donner une citation d'Henri Poincaré qui illustre très bien ce que je viens de raconter :
La mathématique est l'art de donner le même nom à des choses différentes.
Pour créer notre mini-Dobble, on a appelé les dessins des "points" et les cartes des "droites", et on s'est rendu compte qu'on obtient alors un plan projectif fini. Et les points et les droites des plans projectifs sont a priori très différents des points et des droites usuels du plan euclidien !
Bon, et si vous avez du temps à perdre, vous pouvez essayer de créer un Dobble avec $157$ cartes et $157$ dessins, où chaque carte contient $13$ dessins :upside_down_face:.
Et enfin, je remercie la personne qui a peer-review cet article et qui m'a permis de beaucoup l'améliorer.
